Mikrorheologie - Diffusing Wave Spectroscopy (DWS)

Ziel

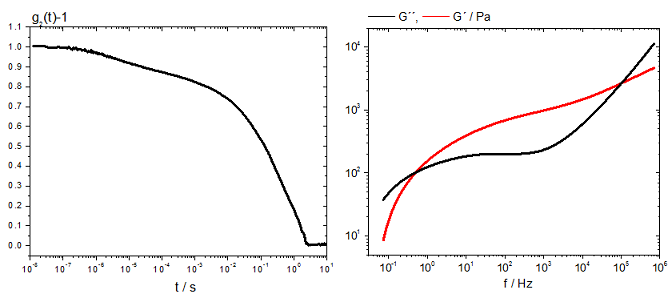
Die DWS ist eine Variante der dynamischen Lichtstreuung, bei der die Vielfachstreuung von Laserlicht analysiert wird. Die Methode eignet sich daher prinzipiell für trübe Materialien wie z. B. konzentrierte Polymerlösungen und Gele, Suspensionen oder Tensidlösungen. Als Streuzentren können entweder gezielt in das zu untersuchende Fluid eingebrachte Tracer oder in der Probe vorhandene Partikel, Tröpfchen oder andere Dichtefluktuationen dienen. Die thermischen Fluktuationen dieser Streuzentren (Brown’sche Bewegung) verursachen zeitliche Intensitätsfluktuationen des Streulichtsignals. Diese Messgröße charakterisiert daher die Dynamik des untersuchten Systems. Da im detektierten Streusignal die Beiträge vieler Streuzentren kumuliert sind, führen schon Verschiebungen der einzelnen Streuer von wenigen nm zu einem messbaren Effekt. Die Methode erlaubt daher die Charakterisierung der Dynamik auf sehr kurzen Zeitskalen ( > 1 ms ), die mit anderen optischen oder mechanischen Methoden nicht oder nur schwer zugänglich sind. Weitere Vorteile sind: geringes Probenvolumen, kurze Messzeit, zerstörungsfreie Prüfung. Die Tracerdynamik erlaubt Rückschlüsse auf die linear-viskoelastischen Eigenschaften des umgebenden Fluids. Bei geeigneter Wahl der Tracer kann ein weiter Modulbereich erfasst werden ( 10 -1 – 10 4 Pa ). Die Methode eignet sich daher auch für die Charakterisierung der Kinetik der Gelbildung oder anderer Strukturänderungen. Die DWS liefert über das Streuvolumen gemittelte Daten, also keine ortsaufgelösten, mikroskopischen Informationen über die Dynamik eines Systems.

 

Messprinzip

Der Aufbau für die DWS besteht aus einem He-Ne Laser, einer temperierten Probenkuvette, einem zwei Photomultipliern und einem Korrelator. Aus den Intensitätsfluktuationen des Streulichts wird zunächst die Intensitäts-Autokorrelationsfunktion g 2 (t) berechnet. Analog zur konventionellen DLS ergibt sich hieraus über die Siegert-Relation die Feld-Autokorrelationsfunktion g 1 (t). Diese wiederum ist mit dem mittleren Verschiebungsquadrat der Streuer  < Δ r 2 (t) >  verknüpft. Mit Hilfe einer verallgemeinerten Stokes-Einstein-Beziehung und einer Laplace-Transformation erhält man schließlich den komplexen Schubmodel G*, bzw. dessen Real- und Imaginärteil G´ und G´´ als Funktion der Frequenz.

 

     

Abbildung 1: DWS-Messplatz   

 

(Infos zum DWS ResearchLab Firma LS Instruments GmbH unter www.lsinstruments.ch/products/dws_rheolab/)

 

Spezifikationen

Probenvolumen:

  0,2 – 3,5 ml in Glasküvetten

Temperaturbereich:

  10 – 70 °C

Frequenzbereich:

  0,1 – 106 Hz

Modulbereich:

  10-1 – 104 Pa

 

Anwendungen

  • Dynamik von synthetischen Polymeren und Biopolymeren in Lösung
  • Biegesteifigkeit von zylindrischen Tensidmizellen
  • Aggregationskinetik von Keramiksuspensionen
  • Gelierung von Joghurt

 

 

Abbildung 2: Messbeispiel: wässriges Polysaccharid Hyaluronan NaHA 30 g/l + NaCl 0,1M. Links: Intensitäts-Autokorrelationsfunktion g2(t)-1; rechts: Frequenzabhängigkeit der linear-viskoelastischen Moduln G’ und G’’.

 

Literatur

  1. C. Oelschlaeger, M. Schopferer, F. Scheffold, and N. Willenbacher: “Linear to branched micelles transition: a rheometry and diffusing wave spectroscopy (DWS) study”, Langmuir 2009, 25 (2), 716-729.
  2. C. Oelschlaeger, P. Suwita, and N. Willenbacher: “Effect of Counterion Binding Efficiency on Structure and Dynamics of Wormlike Micelles“, Langmuir 2010, 26 (10), 7045-7053.
  3. C. Oelschlaeger, M. Cota Pinto Coelho, N. Willenbacher “Flexibility and structure of polysaccharide hyaluronan solutions: a high frequency rheology and diffusing wave spectroscopy study” Biomacromolecules 2013, 14 (10), 3689-3696.
  4. G. Maret and P. E. Wolf, Z. Phys. B 65, 409 (1987)
  5. D. A. Weitz and D. J. Pine, in Dynamic Light Scattering, W. Brown (Ed.), Oxford University Press, New York, (1993)
  6. F. Cardinaux, L. Cipelletti, F. Scheffold and Peter Schurtenberger, giant micelle solutions, Europhys. Lett., 57, 738-744, (2002)
  7. F. Scheffold, P. Schurtenberger
    Light scattering probes of viscoelastic fluids and solids, Soft Materials 1, 139-165, (2003)