Objective
Diffusing wave spectroscopy (DWS) is an extension of dynamic light scattering (DLS), in which multiple light scattering is analysed. The method is therefore suitable in principle for turbid materials e.g. concentrated polymer solutions and gels, suspensions or surfactant solutions. Scattering centers can either be tracers that have been brought into the fluid or particles, droplets or other density fluctuations already existing in the sample. The thermal fluctuations of these scatterers (Brownian motion) cause temporal intensity fluctuations of the scattered light signal. This phenomenon is used to characterize the viscoelastic properties of the surrounding fluid. Since in the detected signal the contributions of many tracers are cumulated, shifts of only a few nm of the individual scatterers already lead to a measurable effect. This method allows therefore characterisation of the dynamics on very short time scales ( > 1 ms ), which are hardly accessible with other optical or mechanical methods. Other advantages are: small sample volume, short measurement time, no applied strain. With suitable choice of the tracers a large module range can be measured ( 10 -1 – 10 4 Pa ). The method is therefore suitable also for the characterisation of kinetics of gel formation or other structural changes. DWS provides data averaged over the scattering volume and no spatially resolved microscopic information about the dynamics of a system.
Operating Principle
Our DWS setup includes a He-Ne Laser, a temperature controlled water bath, two photomultipliers and a correlator. The quantity measured is the correlation function of the temporal fluctuations of the scattered light g 2 (t). As with conventional DLS, the Siegert relation allows to determinate the field autocorrelation function g 1 (t). This quantity is connected to the average mean-square displacement of the scattering particles < Δ r 2 (t) >. Using the generalized Stokes-Einstein relation and the Laplace transformation, the complex shear modulus G* can be determinate, e.g. the linear viscoelastic moduli G´ und G´´ in function of the frequency.
Fig. 1: DWS-setup
(Information about the DWS ResearchLab of the company LS Instruments GmbH: www.lsinstruments.ch/products/dws_rheolab/)
Specifications
|
Sample volume: |
0.2 - 3.5 ml in standard precision glass cell |
|
Temperature range: |
10 – 70 °C |
|
Frequency range: |
0,1 – 106 Hz |
|
Moduli range: |
10-1 – 104 Pa |
Applications
- Relaxation dynamics of synthetic polymers and biopolymers in solution
- Bending stiffness of cylindrical wormlike micelles
- Kinetic of aggregation of ceramic suspensions
- Gelation of yoghurt
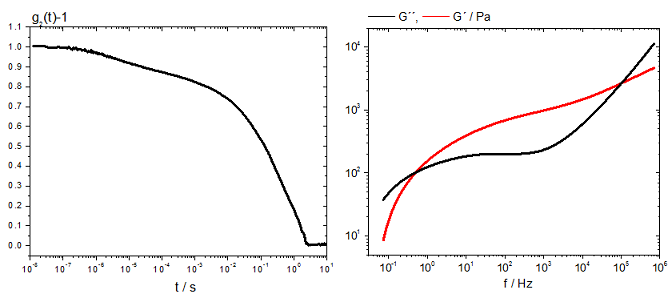
Fig. 2: Measurement example: aqueous polysaccharide Hyaluronan NaHA 30 g/l + NaCl 0,1M.
Intensity autocorrelation function g2(t)-1 (left), frequency dependence of linear viscoelastic moduli G’ and G’’ (right).
Literature
- C. Oelschlaeger, M. Schopferer, F. Scheffold, and N. Willenbacher, “Linear to bran¬ch¬ed micelles transition: a rheometry and diffusing wave spectroscopy (DWS) study”, Langmuir 2009, 25 (2), 716-729.
- C. Oelschlaeger, P. Suwita, and N. Willenbacher “Effect of Counterion Binding Efficiency on Structure and Dynamics of Wormlike Micelles“, Langmuir 2010, 26 (10), 7045-7053.
- C. Oelschlaeger, M. Cota Pinto Coelho, N. Willenbacher, “Flexibility and structure of polysaccharide hyaluronan solutions: a high frequency rheology and diffusing wave spectroscopy study” Biomacromolecules 2013, 14 (10), 3689-3696.
- G. Maret and P. E. Wolf, Z. Phys. B 65, 409 (1987)
- D. A. Weitz and D. J. Pine, in Dynamic Light Scattering, W. Brown (Ed.), Oxford University Press, New York, (1993)
- F. Cardinaux, L. Cipelletti, F. Scheffold and Peter Schurtenberger, giant micelle solutions, Europhys. Lett., 57, 738-744, (2002)
- F. Scheffold, P. Schurtenberger
Light scattering probes of viscoelastic fluids and solids, Soft Materials 1, 139-165, (2003)