Objective
High frequency rheometry provides insight into microstructure, interactions and local dynamics of complex fluids. This is of great interest both for pure and applied research. In the case of concentrated colloidal suspensions e.g. the high frequency modulus probes thermodynamic particle interactions and can be directly correlated to suspension stability. For polymer or surfactant solutions the hierarchical relaxation of structural elements results in characteristic scaling regimes for the high frequency moduli which can be related to microscopic features like chain stiffness, molecular architecture or solvent-polymer interactions. The location of the high frequency regime on an absolute scale of course strongly depends on the characteristic features of the respective fluid and typically extends from 10 to 106 Hz. Conventional rotational rheometers are usually limited to frequencies < 102 Hz and for complex fluids time-temperature superposition is generally not suitable to extend this frequency range. In these cases oscillatory squeeze flow and torsional resonance oscillation give direct access to G ' and G '' in the frequency range between 0.1 Hz -100 kHz.
Operating Principle
Oscillatory Squeeze Flow
In the Piezoelectric Axial Vibrator (PAV) the dynamic squeeze flow is excited by four piezoelectric transducers controlled by a lock-in amplifier, four different piezos take up the response signal. The moduli G ' and G '' are computed from the relationship of the voltage signals with and without sample and the corresponding phase shift.

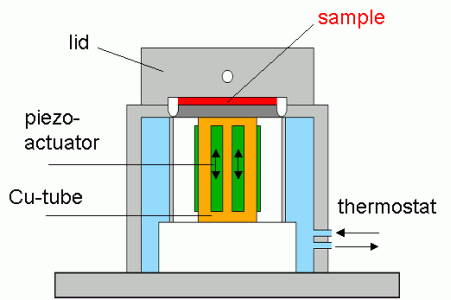
Fig. 1 Piezoelectric axial vibrator - photo and schematic drawing
Specifications
| Sample volume: | ab 10 µl air tight |
| Frequency range: | 1 - 7000 Hz |
| Gap: | 0,01 - 1 mm |
| Temperature range: | 5 – 95 °C |
| Oscillation amplitude: | max. 5 nm (deformation γ < 0,001) |
Operating Principle
Torsional Resonance Oscillation
Two piezoelectrically driven titanium resonators (cylindrically and dumbbell shaped) operating at four different frequencies between 8 kHz and 60 kHz are available. A lock-in amplifier is used to determine their resonance characteristics. G' and G'' of a fluid surrounding a resonator are calculated from the corresponding shift of the resonance frequency and the broadening of the resonance curve as compared to the unperturbed oscillation in air.

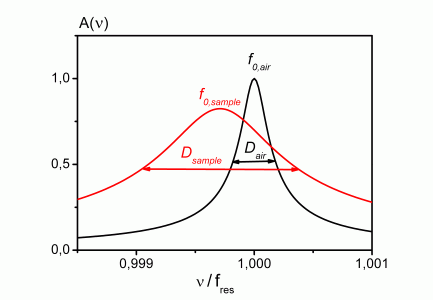
Fig. 2 cylinder and dumbbell resonators as well as resonance curve with/without sample
Specifications
| Sample volume: | 10 – 40 ml |
| Frequencies: | 8, 19, 31, 59 kHz |
| Oscillation amplitude: | approx. 50 nm (deformation γ < 0,01) |
| Viscosity range: | 0,001 – 10 Pa s |
| Temperature range: | 5 – 95 °C |
Applications
For concentrated suspensions the loss modulus G’ is linked directly with the colloidal interactions of the suspended particles and h’ is solely controlled by the hydrodynamic volume. Thus the method can be used for:
- In-situ characterization of interaction potential - no artefacts from sample preparation, sensitive to each kind of interaction on the length scale of the mean particle separation
- Determination of the hydrodynamic particle volume, in particular sensitive to particle permeability/porosity or swelling
- The frequency dependency of the storage modulus of a concentrated dispersion can be used as a "finger print" (fig. 4) for the identification of the stabilization mechanism.
The relaxation behaviour of polymer solutions is characterized by different scaling laws in the high frequency range. For semiflexible polymers e.g. biopolymers (DNA, Myosin, F-actin) or self-assembling systems like cylindrical surfactant micelles the bending stiffness or persistence length can be determined from the high frequency moduli.
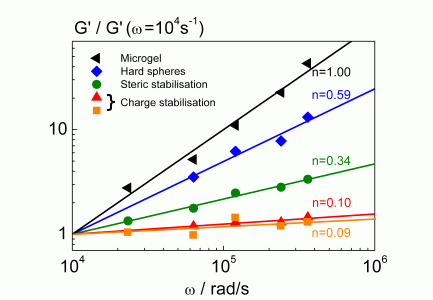 |
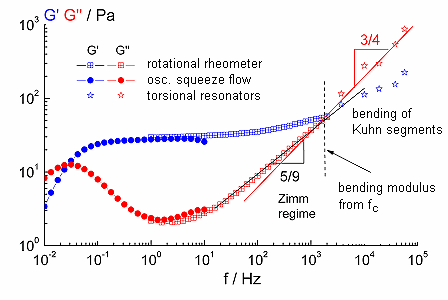 |
|
Fig. 3 finger print of colloidal interactions in concentrated suspensions |
Fig. 4 relaxation spectrum of a viscoelastic surfactant solution (CPyCl/NaCl), Maxwell regime (f < 1 Hz), plateau zone (1 Hz < f < 100 Hz), short range relaxation processes (f > 103 Hz) |
Literature
J. Crassous, R. Régisser, M. Ballauff, N. Willenbacher, J. Rheol. 49(4), 851-864 (2005)
G. Fritz, N. Willenbacher, and N.J. Wagner, J. Rheol. 47(2), 303-319 (2003)
G. Fritz, V. Schädler, N. Willenbacher, and N.J. Wagner, Langmuir 18, 6381-6390 (2002)
F.M. Horn, W. Richtering, J. Bergenholtz, N. Willenbacher, N.J. Wagner, J. Colloid Interface Sci. 225, 166-178 (2000)
J. Bergenholtz, F. M. Horn, W. Richtering, N. Willenbacher, N. J. Wagner, Physical Review E, Rapid Communications, 58 (4) (1998), 4088-4091
